12.2.2 Gates
Gates are electronic versions of the mechanical switches introduced above. Some gates have multiple inputs, but all gates have a single output. Just as the switches and light bulbs of the previous examples were always in either of two states, the inputs and outputs of gates are confined to two voltage states. The voltage of every input to the gate, as well as the output from the gate, must be either high (5 volts) or low (ground). We use the symbol “1” to represent the high voltage state and “0” to represent the low voltage state.
There are three basic kinds of logic gates: and gates, or gates, and not gates. An and gate has two inputs and one output. The output is “1” (high) only when both inputs are “1” (high). In all other cases the output of and is “0” (low). Figure 12.5 presents the standard symbol for an and gate along with its definition in the form of a truth table. The inputs to the gate have been labeled “A” and “B”, while the output has been labeled “Z”.
A truth table defines the meaning of a gate, or circuit, by listing every possible configuration of inputs along with the corresponding output. Traditionally, inputs are listed on the left side of the table with the output on the right. Each row of the truth table represents one configuration that the circuit can be in. Truth tables for circuits with n inputs will always have exactly 2n rows, one for each possible configuration of the inputs.
Since and has two inputs, its truth table will contain 22 = 4 rows. The first row of the truth table of Figure 12.5 represents the situation in which both inputs to the and gate are low. In this case the output will be low as well. The second and third rows cover the cases in which one of the inputs is high and the other is low. In line two, the first input is low and the second is high. In line three, the first input is high and the second is low. In either case, the output is low. The final row of the table represents the situation in which both inputs are high. In this case, the output will be high as well.
The functionality of the and gate can be implemented by the series circuit introduced in Section 12.2.1. In fact, you may have noticed that the truth table for and is identical to the table of values given in Figure 12.3 for two switches in series, if “open” / “off” is replaced by “0” and “closed / “on” is replaced by “1”.
Figure 12.5: An and gate
Figure 12.6: An or gate
The reason that truth tables are called “truth tables” is that if “1” is taken to mean “true” and “0” is taken to mean “false” then the output of the table defines the circumstances under which the specified logical operation is true. For example, in common English usage, “A and B” will be true only when both A and B are true. The statement: “My cat is old and fat” is only true when the cat in question is both “old” and “fat”. If my pet cat were either young, or skinny, or both, then the statement about her would be false.
The thing that is so exceedingly cool about logic gates, and the circuits that implement them, is that very simple devices, such as those presented in Section 12.2.1, can capture small parts of what humans consider “logical reasoning”. As you can well imagine, this idea caused great excitement when first discovered. We’ll have much more to say about logic and its relation to intelligent behavior in Chapter 14: Computing and Intelligence. For now, let’s return to the discussion of the basic logic gates.
The standard symbol for an or gate and its definition via truth table are given in Figure 12.6. Or gates are similar to and gates in that they have two inputs and a single output. The output of the or gate is “1” whenever either, or both, of the inputs are “1”. The only case in which the output of or is “0” is when both of the inputs are “0”.
An or gate can be implemented by the parallel circuit of Figure 12.4. This can be seen by comparing the circuit’s table of values to the truth table of Figure 12.6 – making the necessary substitutions of “0” for “open” / “off” and “1” for “closed / “on”.
You should convince yourself that the behavior of the or gate captures the semantics of the word or as it is commonly used. The statement: “My cat is either on the couch or under the bed.” is true if either the phrase “my cat is on the couch” is true or the phrase “my cat is under the bed” is true. The original statement is false only when neither of these phrases is true.
Figure 12.7: A not Gate
The third basic logic gate is the not gate. It has a single input and a single output. The output is the inverse of the input, as shown in the truth table in Figure 12.7. Note that this truth table consists of only two rows, rather than four as was the case with and and or . This is consistent with the claim that truth tables contain exactly 2n rows for an n input circuit. Since not takes in only a single input, there are only two possible configurations that the gate can be in.
As with and and or , the behavior of the not gate captures the semantics of the word. If the sentence: “My cat is black.” is true, then the sentence “My cat is not black.” would be false. And vice versa.
In exercise 3 of Section 12.2.1, the following circuit, which uses three switches, was presented:
It is natural to ask at this point what an equivalent circuit consisting of logic gates would look like. Since switches A and B are in parallel, this portion of the circuit can be represented using an or gate. The output of that part of the circuit is in series with C, so it can be modeled with an and gate. The logic gate circuit shown below is thus equivalent to the switch circuit given above.
Exercises for Section 12.2.2
-
Develop the complete truth table for the following circuit:
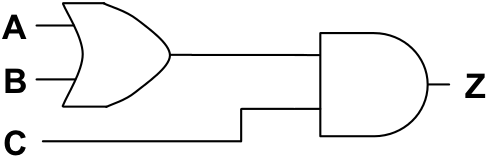
-
Draw a circuit using switches, a power supply, and a light bulb for the following logic circuit:
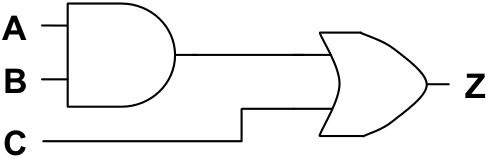
-
Develop the complete truth table for the circuit of problem 2.